Het internet staat alweer op z’n kop door een simpele, maar verwarrende rekensom: 8 ÷ 2(2+2). Op het eerste gezicht lijkt het een makkelijk vraagje uit groep 8, maar het blijkt een stuk lastiger dan verwacht. Iedereen denkt het juiste antwoord te hebben, maar de meningen verschillen enorm: is het 1 of toch 16?
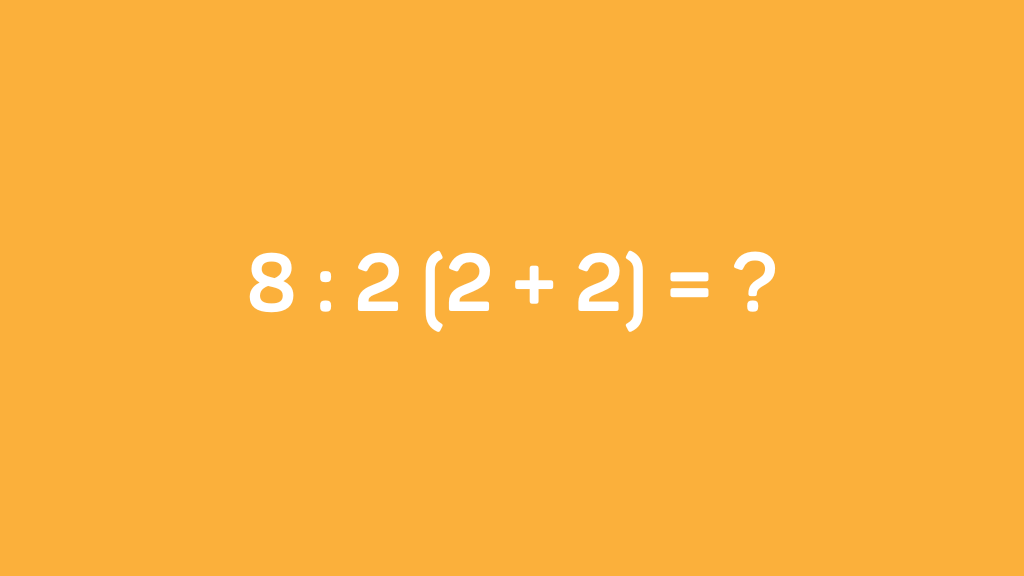
Waarom deze rekensom zo verwarrend is
Wiskunde is normaal gesproken keihard en eenduidig. Toch zorgt deze som voor verwarring. Dat komt doordat het niet alleen gaat om de juiste berekening, maar ook om de volgorde van de stappen. En laat dat nou net het punt zijn waar mensen het vaak fout doen of anders interpreteren.
De som ziet er zo uit:
8 ÷ 2(2+2)
De verwarring ontstaat na het oplossen van de haakjes. Daarna blijven er twee manieren over om de rest van de som op te vatten. Dat levert dus twee totaal verschillende uitkomsten op. Welke is nou juist?
Stap 1: Haakjes eerst
Eén ding is zeker: je begint met het oplossen van de haakjes.
2 + 2 = 4
De som wordt dan:
8 ÷ 2(4)
En hier gaat het mis. Want wat betekent 2(4)? Is dat:
-
8 ÷ (2 × 4), dus eerst 2 keer 4 doen en dan 8 gedeeld door 8?
-
Of is het (8 ÷ 2) × 4, dus eerst 8 gedeeld door 2 en dan dat keer 4?
Twee kampen, twee uitkomsten
Mensen die zeggen dat het antwoord 1 is, pakken het zo aan:
8 ÷ 2(4) wordt gelezen als 8 ÷ (2 × 4)
Ze rekenen eerst 2 × 4 = 8
Daarna: 8 ÷ 8 = 1
Anderen zeggen dat het antwoord 16 is, en die lezen het zo:
8 ÷ 2(4) wordt opgevat als (8 ÷ 2) × 4
Eerst: 8 ÷ 2 = 4
Dan: 4 × 4 = 16
Beide routes lijken logisch. En daar zit precies het probleem.
Wat zeggen de moderne rekenregels?
Volgens de huidige rekenregels worden vermenigvuldigen en delen als gelijkwaardig beschouwd. Dat betekent dat je deze bewerkingen uitvoert van links naar rechts. Dus als je na de haakjes 8 ÷ 2 × 4 overhoudt, dan:
-
Doe je eerst 8 ÷ 2 = 4
-
Daarna: 4 × 4 = 16
Deze volgorde is tegenwoordig standaard in rekenonderwijs en bij de meeste digitale rekenmachines en wiskundeprogramma’s.
Waarom denken sommige mensen dan dat het 1 is?
Dat heeft alles te maken met hoe de som opgeschreven is. De notatie 2(4) lijkt soms op een soort vermenigvuldiging die bij elkaar hoort, alsof er onzichtbare haakjes staan. Daardoor denken sommigen dat het een blok is, waardoor je eerst 2 × 4 doet en dat dan als geheel deelt in de som.
Als de som op die manier bedoeld was, had hij eigenlijk zo moeten worden geschreven:
8 ÷ [2(4)] of 8 ÷ (2 × 4)
Maar dat staat er dus niet. Er staan geen extra haakjes om dat deel van de som, dus volgens de standaardregels moet je van links naar rechts rekenen.
Een kwestie van notatie
Deze hele discussie gaat eigenlijk minder over wiskunde en meer over duidelijkheid. Want als iets onduidelijk genoteerd is, kan zelfs een simpele som leiden tot discussie.
Je zou kunnen zeggen dat de fout niet zit in het rekenen, maar in hoe de som op papier staat. Als iedereen dezelfde volgorde bedoelde, had de som gewoon met haakjes geschreven moeten worden.
Wat kun je hiervan leren?
Het belangrijkste wat je uit dit soort virale puzzels kunt halen, is dat heldere notatie alles is in de wiskunde. Wanneer je sommen opstelt of leest, wees dan duidelijk over welke bewerking eerst moet. En als je ooit zelf iets met formules doet, voeg dan haakjes toe om twijfel te voorkomen.
Zo voorkom je dat jouw rekensom viral gaat – en niet op een goede manier.
Dus… wat is het juiste antwoord?
Als je de standaardvolgorde van bewerkingen volgt, en van links naar rechts rekent na het oplossen van de haakjes, dan krijg je:
8 ÷ 2(2+2)
→ 8 ÷ 2 × 4
→ 4 × 4
→ 16